Manuals Forum - Expanded Thread Page
Subject: Sherman Fork Lift - Installation Instructions to Dealers
[Back] [Return to Top of Forum]
| Ed Gooding (VA) |
Posted 12-17-2008 at 06:08:38 [URL] [DELETE]
[Reply] [Email] This is a 1955 Service Letter sent to dealers to instruct them how to install the Sherman Fork Lift.  Please review our tutorial in our How-To's - Misc. section on how to best capture posted images to your PC to save, edit and print as you need. Printing them from your browser (Internet Explorer, FireFox, etc.) will NOT work reliably. |
|---|---|
| Ed Gooding (VA) |
Posted 12-17-2008 at 06:10:08 [URL] [DELETE]
[Reply] [Email]     |
| Ed Gooding (VA) |
Posted 12-17-2008 at 06:13:06 [URL] [DELETE]
[Reply] [Email]     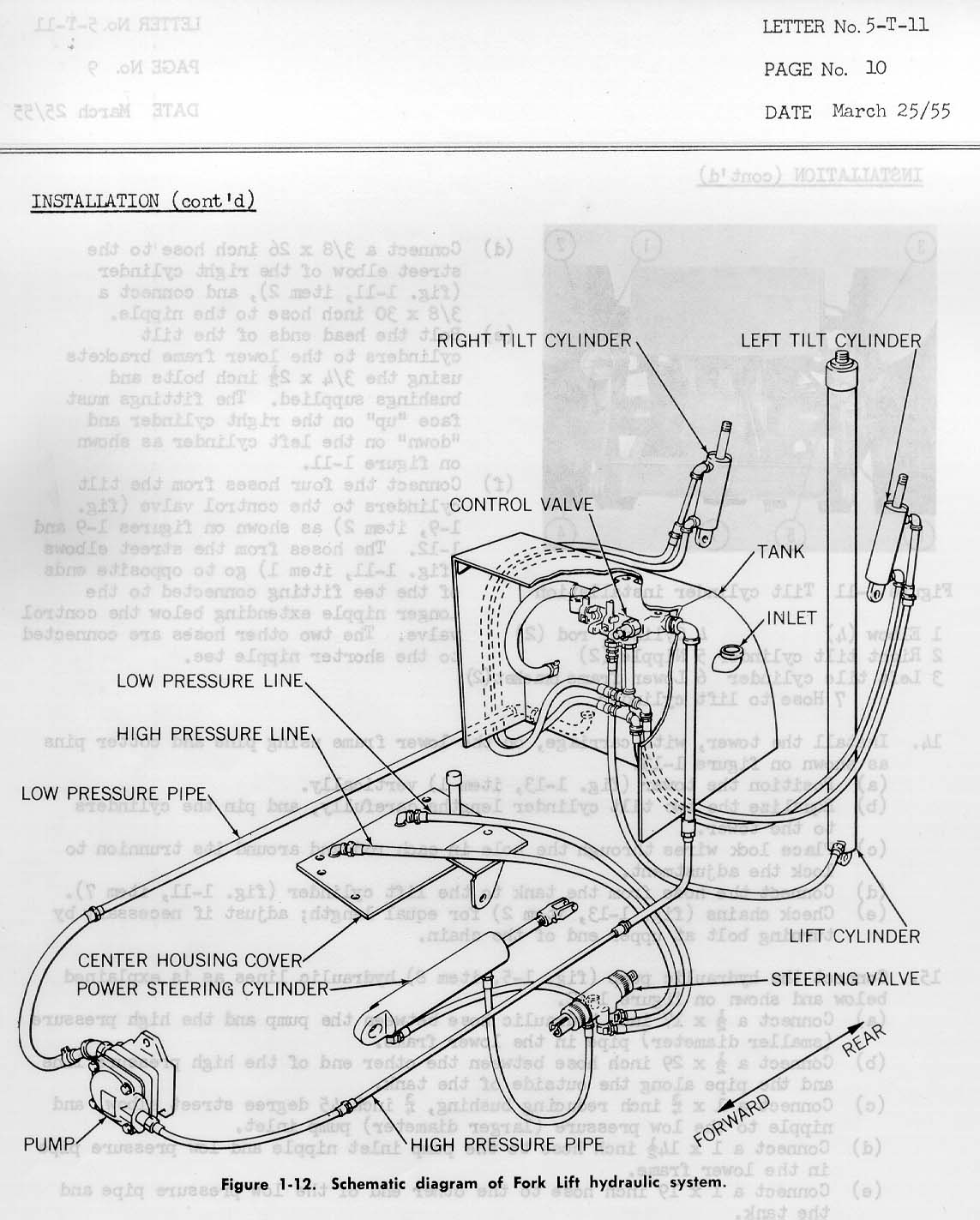 |
| Ed Gooding (VA) |
Posted 12-17-2008 at 06:14:48 [URL] [DELETE]
[Reply] [Email]   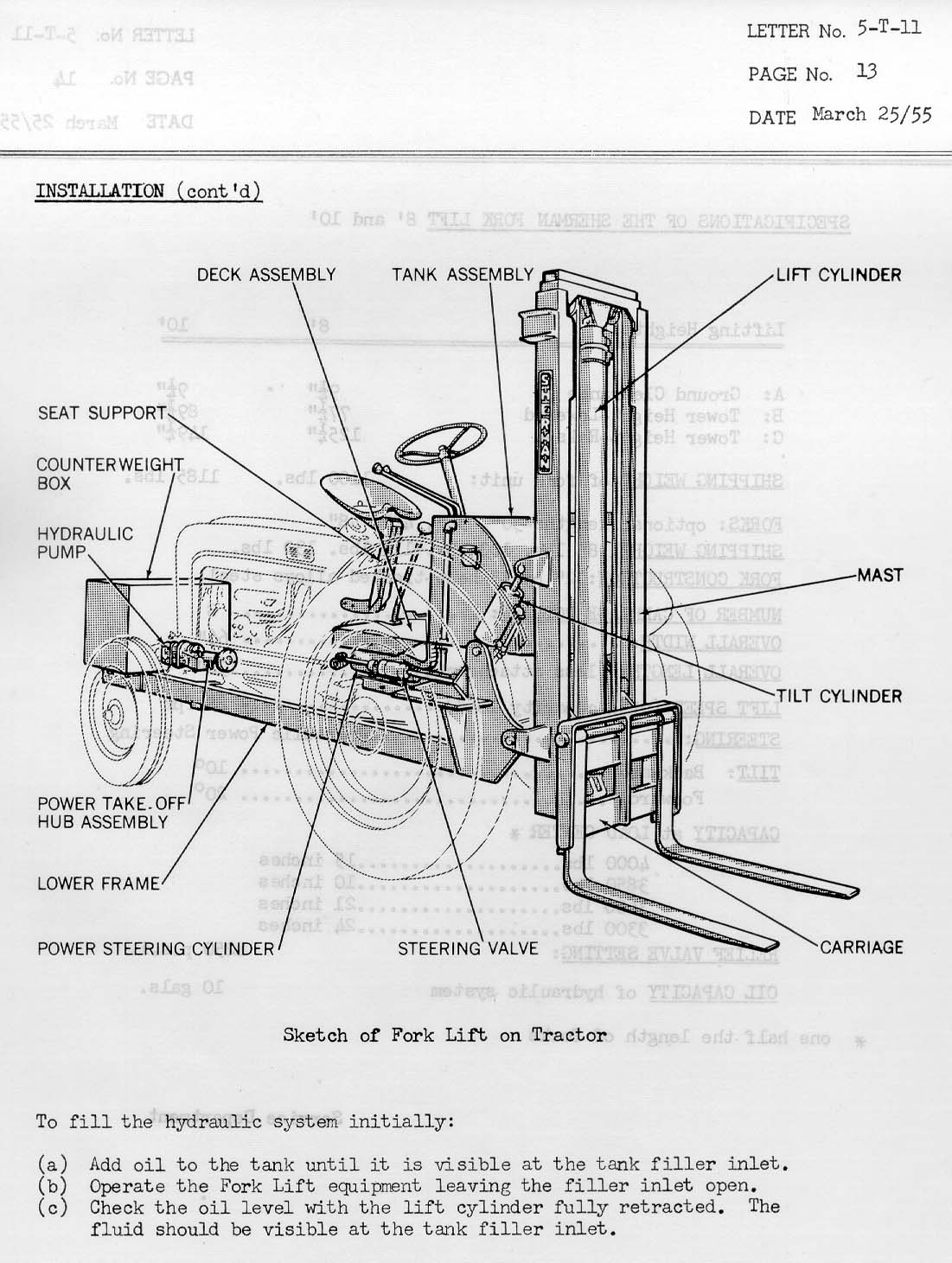  |
| Ed Gooding (VA) |
Posted 12-17-2008 at 06:16:19 [URL] [DELETE]
[Reply] [Email]  |
| Ed Gooding (VA) |
Posted 12-17-2008 at 06:17:06 [URL] [DELETE]
[Reply] [Email]  |
| Ed Gooding (VA) |
Posted 12-17-2008 at 06:18:59 [URL] [DELETE]
[Reply] [Email]  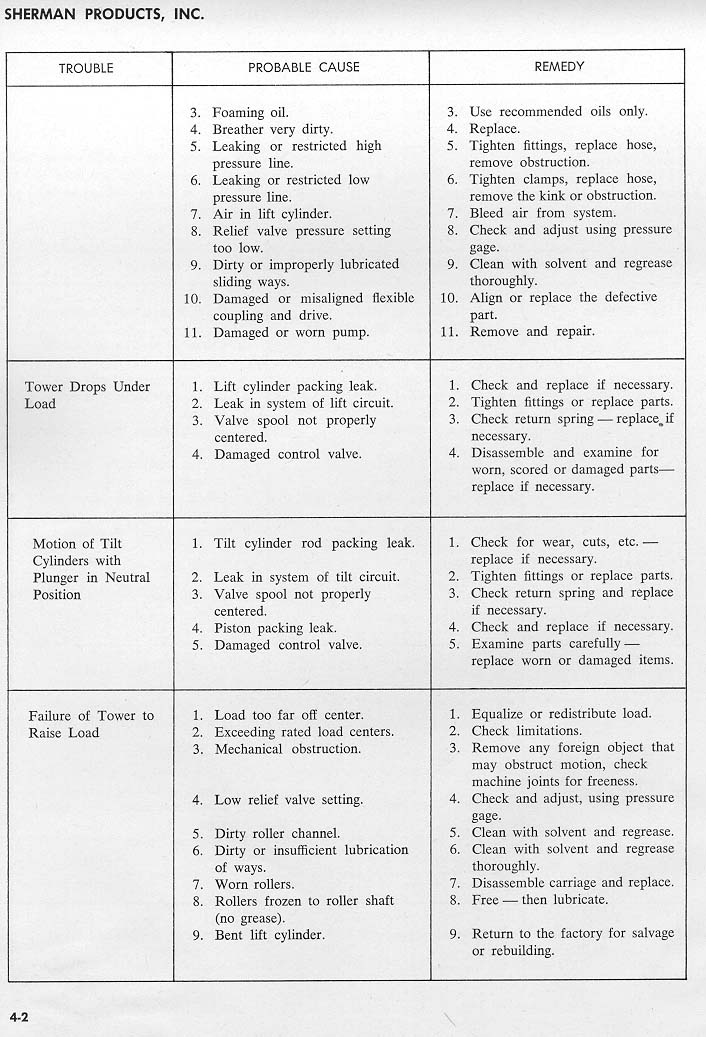 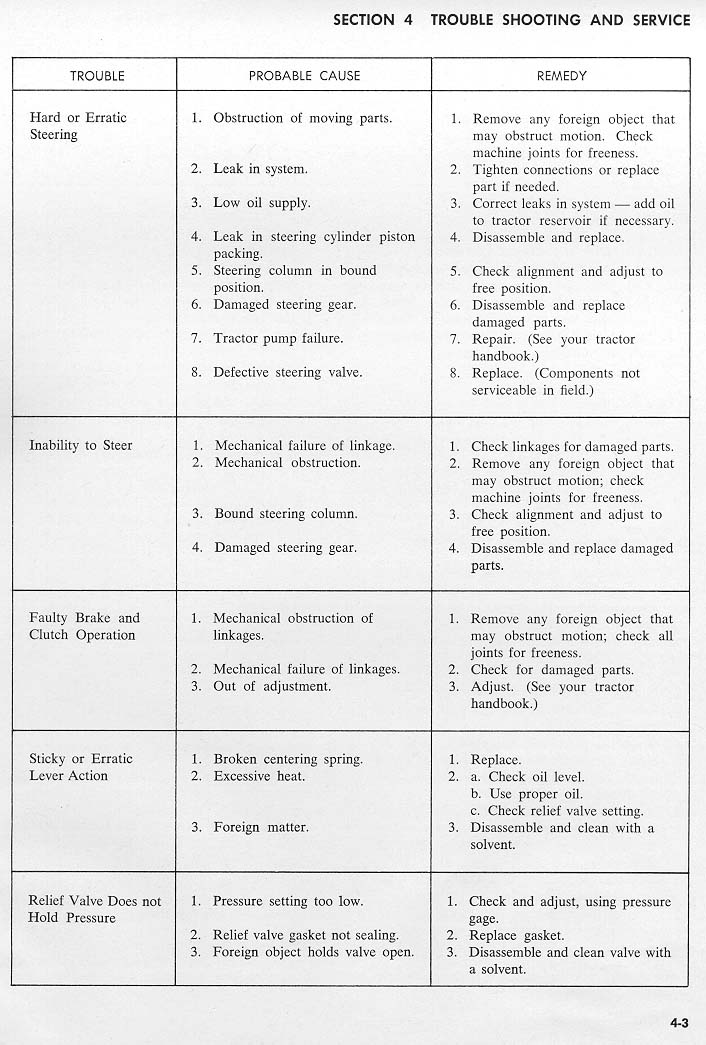     |
[Back] [Return to Top of Forum]